The Shape of Music | The Circle of Fifths Part 2
Written by Mete Bakircioglu; Edited by Jackson Poling
This is the second section of a two-part lesson where we dissect and analyze the circle of fifths, the treasure map to music theory. In the first half, we started learning about how this diagram maps out the relationships among the 12 unique tones of Western music. We examined its history and how it displays key signatures. Join me as we take a look at a few more functions of the circle of fifths.
Listen to the podcast:
Uses of the Circle of Fifths:
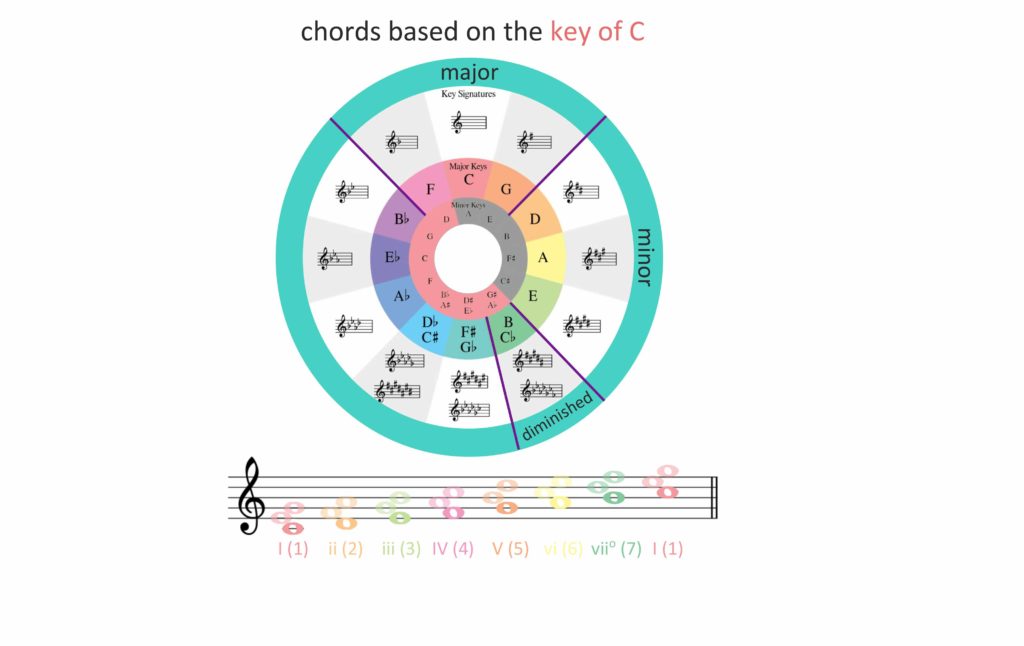
Chords:

The first is how it shows the chords available in a key. Let’s take our familiar friend C for example. We know that the C major chord is a part of the key of C. Look at the two keys on either side of C: F and G. These two chords are also major. Now going clockwise around the circle three positions, we find the minor chords in the key of C: D , A, and E. The seventh and last chord in the key of C is the B diminished chord. So mapping out the chords in the key of C based on the circle, we find that C is major, D is minor, E is minor, F is major, G is major, A is minor, and B is diminished. Here’s the wild part: this pattern of major, minor, minor, major, major, minor, diminished holds true for any major key.
The Harmonic Series:
Another core concept of the circle of fifths is the harmonic series. The harmonic series is a rainbow of related pitches that sound when you play a note. If I play a C for example, you would think that you’re only hearing this one tone… but you’re not. You’re actually hearing a series of what are called overtones, which are kind of like phantom notes that give a note on an instrument its unique timbre, or quality of sound. We know from the episode on instruments that music can be produced by strings vibrating at different speeds or frequencies. Well, when a string is played, it’s vibrating not only at the full length of the string, but it’s also vibrating at half the length, a third the length, a quarter of the length, and so on. Each of these wavelengths produces a different sound or overtone. Check out the video below to watch me prove the harmonic series is real (I guarantee it’ll blow your mind).
Relative Minor Keys:
Another function of the circle is that it shows relative minor keys. What I mean by that is every major key has what’s called a relative minor key associated with it. A relative minor has the same key signature as its relative major. I like to think of it as the major key’s shadow. For example, the relative minor of C major is A minor. A minor has the same notes as C major. The relative minors are written on the inside of the circle in lower case letters. One famous example of a piece that changes from its relative minor to the major key is the theme from Tchaikovsy’s Swan Lake. It starts out in B minor (Play audio 1 below). Here it switches to D major, the relative major (audio 2). Now we’re back to B minor in an epic arrival of the brass instruments (audio 3). The use of relative majors and minors can make the listener feel like they have passed over to the shadow of what they were listening to before. It’s still the same piece and the same key signature but the atmosphere has become inverted. In this piece, Tchaikovsky takes us through a weighted sadness, followed by a ray of hopefulness in D major, just to be overtaken by another, heavier dreadfulness in the return to B minor.
Modes:
The last offering of the circle for today has to do with Greek modes. What if we took A major’s key signature and made a scale on D? Well that’s what we would call a mode. From the circle, I know that A has three sharps: F, C, and G. So let’s play a D scale with these three sharps: (audio 4). This is called the lydian mode, and it’s where you raise the fourth note of a scale. It’s my favorite mode because it sounds dreamy and kind of magical. In total, we’ve got seven Greek modes: ionian (which is also our familiar friend: the major scale) (audio 5), dorian (audio 6), phrygian (audio 7), lydian (audio 8), mixolydian (audio 9), aeolian (which is also the relative minor of a key) (audio 10), and finally, locrian (audio 11).
Greek modes were studied 2,000 years ago by the most well known philosophers like Plato and Aristotle as having effects on mood and character. This quote from Aristotle’s book Politics describes these effects: “The musical modes differ essentially from one another, and those who hear them are differently affected by each. Some of them make men sad and grave, like the so called Mixolydian; others enfeeble the mind, like the relaxed modes; another, again, produces a moderate or settled temper, which appears to be the peculiar effect of the Dorian; and the Phrygian inspires enthusiasm.” The philosopher argues that the music you listen to shapes who you are, which is any idea still believed today. In the late 1900s, people thought that kids listening to rock and roll music were influenced to become more violent or disruptive. Aristotle is basically saying what we’ve been learning: each of these modes has a different color, just like each key has its own color. The more you experiment with each one, the easier it’ll be for you to hear the similarities and differences in the colors.

Be sure to check out the podcast version of this episode for more on the circle of fifths—our musical treasure map! While this is the last episode of new content, our musical journeys are not over yet. Be on the lookout for a recap episode, where we talk through all of what we learned these past five episodes and wrap up this series with a nice bowtie.

About the author:
Mete Bakircioglu is a senior at Lakeridge High School who strives to empower his generation in his American and international communities through promoting the arts and celebrating cultures. His primary academic interest is political science, and understanding how people can shape society for the betterment of underrepresented communities. As a member of his school’s speech and debate team, Mete loves to study the art of argumentation. Outside of school, he enjoys going on afternoon walks with his dog Lucy and serving on his school district’s school board as the student representative for his high school. Mete also enjoys playing piano and violin. He is currently preparing for OMTA Syllabus evaluation for level 10 piano.
